|
| 1 | +# LeetCode 第 142 号问题:环形链表 II |
| 2 | + |
| 3 | +> 本文首发于公众号「图解面试算法」,是 [图解 LeetCode ](<https://github.com/MisterBooo/LeetCodeAnimation>) 系列文章之一。 |
| 4 | +> |
| 5 | +> 同步博客:https://www.algomooc.com |
| 6 | +
|
| 7 | +今天分享的题目来源于 LeetCode 上第 142 号问题:环形链表II。题目难度为 Medium 。 |
| 8 | + |
| 9 | +### 题目描述 |
| 10 | + |
| 11 | +给定一个链表,返回链表开始入环的第一个节点。 如果链表无环,则返回 `null`。 |
| 12 | + |
| 13 | +为了表示给定链表中的环,我们使用整数 `pos` 来表示链表尾连接到链表中的位置(索引从 0 开始)。 如果 `pos` 是 `-1`,则在该链表中没有环。 |
| 14 | + |
| 15 | +**示例 1:** |
| 16 | + |
| 17 | +``` |
| 18 | +输入:head = [3,2,0,-4], pos = 1 |
| 19 | +输出:tail connects to node index 1 |
| 20 | +解释:链表中有一个环,其尾部连接到第二个节点。 |
| 21 | +``` |
| 22 | + |
| 23 | +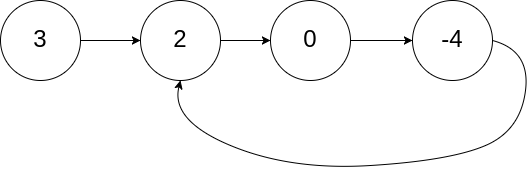 |
| 24 | + |
| 25 | +**示例 2:** |
| 26 | + |
| 27 | +``` |
| 28 | +输入:head = [1,2], pos = 0 |
| 29 | +输出:tail connects to node index 0 |
| 30 | +解释:链表中有一个环,其尾部连接到第一个节点。 |
| 31 | +``` |
| 32 | + |
| 33 | +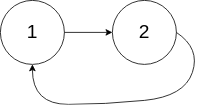 |
| 34 | + |
| 35 | +**示例 3:** |
| 36 | + |
| 37 | +``` |
| 38 | +输入:head = [1], pos = -1 |
| 39 | +输出:no cycle |
| 40 | +解释:链表中没有环。 |
| 41 | +``` |
| 42 | + |
| 43 | + |
| 44 | + |
| 45 | +**进阶:** |
| 46 | + |
| 47 | +你是否可以不用额外空间解决此题? |
| 48 | + |
| 49 | +### 题目解析 - 哈希表 |
| 50 | + |
| 51 | +普通解法就是利用哈希表保存访问过的节点, 同时遍历过程中检查哈希表中是否已存在相同的节点 |
| 52 | + |
| 53 | +### 代码实现 |
| 54 | + |
| 55 | +```javascript |
| 56 | +/** |
| 57 | + * JavaScript 描述 |
| 58 | + * 哈希表方法 |
| 59 | + */ |
| 60 | +var detectCycle = function(head) { |
| 61 | + let res = [ ]; |
| 62 | + while (head !== null) { |
| 63 | + if (res.includes(head)) { |
| 64 | + return head; |
| 65 | + } |
| 66 | + res.push(head); |
| 67 | + head = head.next; |
| 68 | + } |
| 69 | + return null; |
| 70 | +}; |
| 71 | +``` |
| 72 | + |
| 73 | +### 复杂度分析 |
| 74 | + |
| 75 | +- 时间复杂度:**O(n)** |
| 76 | +- 空间复杂度:**O(n)** |
| 77 | + |
| 78 | +### 题目解析 - Floyd 算法 |
| 79 | + |
| 80 | +Floyd算法 可以达到常量空间解决此问题. |
| 81 | + |
| 82 | +我在维基百科找到了这个算法描述, 在此引用一下. |
| 83 | + |
| 84 | +**Floyd判圈算法**(**Floyd Cycle Detection Algorithm**),又称 **龟兔赛跑算法**(**Tortoise and Hare Algorithm**),是一个可以在[有限状态机](https://zh.wikipedia.org/wiki/有限状态机)、[迭代函数](https://zh.wikipedia.org/wiki/迭代函数)或者[链表](https://zh.wikipedia.org/wiki/链表)上判断是否存在[环](https://zh.wikipedia.org/wiki/環_(圖論)),求出该环的起点与长度的算法。 |
| 85 | + |
| 86 | +如果有限状态机、迭代函数或者链表存在环,那么一定存在一个起点可以到达某个环的某处 ( 这个起点也可以在某个环上 )。 |
| 87 | + |
| 88 | +初始状态下,假设已知某个起点节点为节点 *S*。现设两个指针 `t` 和 `h` ,将它们均指向 *S*。 |
| 89 | + |
| 90 | +接着,同时让 `t` 和 `h` 往前推进,但是二者的速度不同:`t` 每前进 `1` 步, `h` 前进 `2` 步。只要二者都可以前进而且没有相遇,就如此保持二者的推进。当 `h` 无法前进,即到达某个没有后继的节点时,就可以确定从 *S* 出发不会遇到环。反之当 `t` 与 `h` 再次相遇时,就可以确定从 S 出发一定会进入某个环,设其为环 *C*。 |
| 91 | + |
| 92 | +如果确定了存在某个环,就可以求此环的起点与长度。 |
| 93 | + |
| 94 | +上述算法刚判断出存在环 *C* 时,显然 t 和 `h` 位于同一节点,设其为节点 *M*。显然,仅需令 `h` 不动,而t不断推进,最终又会返回节点 *M*,统计这一次t推进的步数,显然这就是环 *C* 的长度。 |
| 95 | + |
| 96 | +为了求出环 *C* 的起点,只要令h仍均位于节点 *M* ,而令t返回起点节点 *S* ,此时h与t之间距为环 *C* 长度的整数倍。随后,同时让 `t` 和 `h` 往前推进,且保持二者的速度相同:`t` 每前进 `1` 步,`h` 前进 `1` 步。持续该过程直至 `t` 与 `h` 再一次相遇,设此次相遇时位于同一节点 *P*,则节点 *P* 即为从节点 *S* 出发所到达的环 *C* 的第一个节点,即环 *C* 的一个起点。 |
| 97 | + |
| 98 | +**看完之后是不是很多疑点, 觉得为什么会这样呢?** |
| 99 | + |
| 100 | +下面用数学简单证明一下 |
| 101 | + |
| 102 | +假设 链表的节点数为 `num`, 从 head 到链表环入口节点数为 `m` (不包含入口节点), 环的节点数为 `n`, 链表环入口设点为 *P* |
| 103 | + |
| 104 | +由此可得 `num = m + n` |
| 105 | + |
| 106 | +假设 慢指针 `Tortoise` (乌龟) 每次走 `1` 个节点, 走了 `x` 步 |
| 107 | + |
| 108 | +假设 快指针 `Hare` (兔子) 每次走 `2` 个节点, 走了 `f` 步 |
| 109 | + |
| 110 | +那么 `f = 2x` |
| 111 | + |
| 112 | +当第一次相遇时, 必然是在环内, 设其点为 *M*, 兔子第一次到达 *M* 点后至少又在环内饶了一圈后追上乌龟, |
| 113 | + |
| 114 | +假设绕了 `k` 圈, 那么可以得到 |
| 115 | + |
| 116 | +`f = x + kn` |
| 117 | + |
| 118 | +兔子到达 *P* 点的步数为 |
| 119 | + |
| 120 | +`f = m + kn` |
| 121 | + |
| 122 | +由 `f = 2x` 和 `f = x + kn` 两个等式可以得到 `x = kn` |
| 123 | + |
| 124 | +由 `f = m + kn` 和 `x = kn` 可知, 乌龟到达 *P* 点还需要走 `m` 步 |
| 125 | + |
| 126 | +而 `m` 的长度正是从 head 到链表环入口节点数的长度, 这是未知的, |
| 127 | + |
| 128 | +那么让兔子从 head 以乌龟的速度走, 乌龟在 *M* 点走, 当兔子和乌龟相遇时即走了 `m` 步, 也就到达了 *P* 节点. |
| 129 | + |
| 130 | +### 动画描述 |
| 131 | + |
| 132 | + |
| 133 | + |
| 134 | +### 代码实现 |
| 135 | + |
| 136 | +```java |
| 137 | +/** |
| 138 | + * JavaScript 描述 |
| 139 | + * Floyd判圈算法 |
| 140 | + */ |
| 141 | +var detectCycle = function(head) { |
| 142 | + if (head == null) { |
| 143 | + return head; |
| 144 | + } |
| 145 | + // 设置快慢指针 |
| 146 | + let tortoise = head, |
| 147 | + hare = head; |
| 148 | + // 检查链表是否有环 |
| 149 | + while (true) { |
| 150 | + if (hare == null || hare.next == null) { |
| 151 | + return null; |
| 152 | + } |
| 153 | + hare = hare.next.next; |
| 154 | + tortoise = tortoise.next; |
| 155 | + if (hare == tortoise) { |
| 156 | + break; |
| 157 | + } |
| 158 | + } |
| 159 | + // 兔子和乌龟第二次相遇找到环入口 |
| 160 | + hare = head; |
| 161 | + while (hare != tortoise) { |
| 162 | + hare = hare.next; |
| 163 | + tortoise = tortoise.next; |
| 164 | + } |
| 165 | + return hare; |
| 166 | +}; |
| 167 | +``` |
| 168 | + |
| 169 | +### 复杂度分析 |
| 170 | + |
| 171 | +- 时间复杂度:**O(n)** |
| 172 | + - 有环情况下, 第一次和第二次相遇, 乌龟步数都小于链表节点数, 因此与链表节点数成线性关系; |
| 173 | + - 无环情况下, 兔子大约需要 n/2 步数到达最后, 因此也与链表节点数成线性关系. |
| 174 | +- 空间复杂度:**O(1)** , 双指针使用常数大小的额外空间 |
| 175 | + |
| 176 | + |
0 commit comments