电路.md

电路

电路基础

最基本的定律

欧姆定律：$U=IR$

电源的有载工作：$U=I(R+r)$， 其中$R$为电源内阻，$r$为负载电阻

功率和功率平衡：$P=UI=EI-R_0I^2$，其中$R_0$为电源内阻

基尔霍夫定律

• KCL：电路中任意一个节点的电流代数和为0，即$\sum\limits_{i=1}^n I_i=0$，其中$I_i$为流入节点的电流；
• KVL：电路中任意一个回路循行方向，回路中电压代数和为0，即$\sum\limits_{i=1}^n U_i=0$，其中$U_i$为沿着循行方向的电压

KCL推广：可以将电路中的某个部分看作一个节点，流入这个部分的电流等于流出这个部分的电流； KVL的电流表示：$\sum E=\sum U_z = \sum IR$，其中$E$为电源电动势，$U_z$为电阻$R$两端的电压。 KVL推广：对于一个开路，开口电压$U$等于电源电动势$E-IR$。

使用基尔霍夫定律时，应先标注出电流电压的参考方向，然后按照参考方向写出方程，最后解方程。

电位的概念：电路中某点相对于参考点的电势差。

电路分析方法

一端口电路：将多个元件看作一个整体，只有两个端口与外部连接。如果两个一端口网络的端口处伏安特性相同，则这两个网络等效。

串联电路：$R=R_1+R_2+\dots+R_n$，$U=U_1+U_2+\dots+U_n$，$I=I_1=I_2=\dots=I_n$

并联电路：$\dfrac{1}{R}=\dfrac{1}{R_1}+\dfrac{1}{R_2}+\dots+\dfrac{1}{R_n}$，$U=U_1=U_2=\dots=U_n$，$I=I_1+I_2+\dots+I_n$

电压源模型：电压源与电阻串联，电压源的电压等于电源电动势，电阻等于电源内阻。

电流源模型：电流源与电阻并联，电流源的电流等于电源电流，电阻等于电源内阻。

二者的互相转化：对于一个电压源$E$内阻$R_0$与$R_L$串联，可视为一个电流源$I_s$内阻$R_0$与$R_L$并联，其中$I_s=\dfrac{E}{R_0}$即$E=I_sR_0$。

支路电流法：对于一个电路，将电路中的每个支路的电流都标注出来，然后根据基尔霍夫定律列出方程，最后解方程。一般来说，对于一个$n$个节点$b$条支路的电路，需要列出$n-1$个KCL方程，$b-n+1$个KVL方程，共$b$个方程，从而解出$b$个未知数（就是各个支路的电流）。

节点电压法：对于两个节点之间的若干支路，电流可通过基尔霍夫定律或者欧姆定律计算，再根据基尔霍夫定律，节点处的电流流入等于流出列方程。

电路定理

Thevenin 定理：任何线性电路都可以用一个电压源和一个串联电阻来等效。

叠加定理：线性电路中，各个电源分别作用时，电路中任意两点间的电压等于各个电源分别作用时，电路中任意两点间的电压的代数和。

叠加定理的使用：将电路中的电源分别作用，求出各个电源作用时的电路中任意两点间的电压，然后将这些电压代数和，即可得到电路中任意两点间的电压。具体来说，将所有不作用的电压源视为短路，所有不作用的电流源视为开路。

Norton 定理：任何线性电路都可以用一个电流源和一个并联电阻来等效。

Thevenin 定理的使用：将两个端口短路，求出两个端口处的电流，即可得到等效电流源的电流，然后将两个端口开路，求出两个端口处的电压，于是可得到等效电流源的内阻。

此外，还有非线性的电阻，伏安特性曲线$U=f(I)$不是一条直线，而是一条曲线，这样的电阻称为非线性电阻。

非线性电阻的分析需要指明工作电流和工作电压，$R=\frac U I$，其中$U$为工作电压，$I$为工作电流，事实上$R$就是在这个点函数$f$的导数，即$R=\dfrac{\mathrm{d}U}{\mathrm{d}I}$。

（待补充）

几个常见的电路元件

电阻

$$ \begin{gather} R=\frac{u}{i} \tag{r.1} \\ u=Ri \tag{r.2} \end{gather} $$

$(r.2)$式子两边乘以$i$并从$0$到$t$积分，得到： $$ \int_0^t ui\mathrm{d}t=\int_0^t Ri^2\mathrm{d}t $$ 表明电能全部消耗在电阻上，即电阻是耗能元件。

电感

$$ \begin{gather} L=\frac{N\Phi}{i} \tag{l.1} \\ \end{gather} $$

电感$L$的单位是亨利（Henry），$1H=1\frac{V\cdot s}{A}$，即$1H$的电感，当电流变化率为$1A/s$时，其两端电压为$1V$。磁通量$\Phi$的单位是韦伯（Weber），$1Wb=1\frac{V\cdot s}{m^2}$，即$1Wb$的磁通量，当磁场变化率为$1T/s$时，其面积为$1m^2$。

当电感元件的磁通量或者电流发生变化时，会产生电动势：

$$ e_L=-\frac{\mathrm{d}\Phi}{\mathrm{d}t}=-L\frac{\mathrm{d}i}{\mathrm{d}t} $$

根据基尔霍夫定律：

$$ \begin{gather} u+e_L=0 \notag \\ u=-e_L=L\frac{\mathrm{d}i}{\mathrm{d}t} \tag{l.2} \end{gather} $$

类似地，$(l.2)$两侧乘以$i$并从$0$到$t$积分，得到：

$$ \int_0^t ui\mathrm{d}t=\int_0^i Li\mathrm{d}i = \frac{1}{2}Li^2 \tag{l.3} $$

可见得电流增大，磁场能量增大，电能转化为磁能，反之磁能转化为电能，也就是说电感不消耗能量，是储能元件。

电容

$$ C=\frac{q}{u} \tag{c.1} \\ $$

电容$C$单位是法拉（Farad），$1F=1\frac{C}{V}$，即$1F$的电容，当电压变化率为$1V/s$时，其两端电荷为$1C$。

当电容元件的电荷量或电压发生变化时，会产生电流：

$$ i_C=\frac{\mathrm{d}q}{\mathrm{d}t}=C\frac{\mathrm{d}u}{\mathrm{d}t} \tag{c.2} $$

（此式子中$u$和$i$参考方向相同）

将$(c.2)$式子两侧乘以$u$再从$0$到$t$积分，得到：

$$ \int_0^t i_Cu\mathrm{d}t=\int_0^u Cu\mathrm{d}u = \frac{1}{2}Cu^2 \tag{c.3} $$

可见得电压增大，电场能量增大，电能转化为电场能量，反之电场能量转化为电能，也就是说电容不消耗能量，是储能元件。

此处的$L$、$C$、$R$可以理解为分别对应于机械系统中的质量$m$、弹簧常数$k$、阻尼系数$b$，三者在此处先规定为常数（实际情况更复杂）；$u$、$i$可以理解为分别对应于机械系统中的位移$x$、速度$v$。

（本章内容下次补充，非考点范围的RC RL电路）

正弦交流电路

几个最基本的公式：

$$ \begin{gather} f=\frac{1}{T} \notag \\ \omega=\frac{2\pi}{T}=2\pi f \notag \end{gather} $$

正弦电流的表示：

$$ i=I_m\sin(\omega t) \tag{ac.i.1} $$

其中$I_m$为电流的最大值，也称为峰值电流，单位是安培（Ampere）；但是实际上，我们更多地使用有效值，即：

$$ \begin{align} \int_0^T i^2R\mathrm{d}t&=I^2_{\mathrm{eff}}RT \\ I_{\mathrm{eff}} &=\sqrt{\frac{1}{T}\int_0^T i^2\mathrm{d}t} \\ &=\sqrt{\frac{1}{T}\int_0^T I_m^2\sin^2(\omega t)\mathrm{d}t} \\ &=\sqrt{\frac{1}{T}\int_0^T \frac{I_m^2}{2}(1-\cos(2\omega t))\mathrm{d}t} \\ &=\sqrt{\frac{I_m^2}{2T}\left(\int_0^T \mathrm{d}t-\int_0^T \cos(2\omega t)\mathrm{d}t\right)} \\ &=\sqrt{\frac{I_m^2}{2T}\left(T-0\right)} \\ &=\sqrt{\frac{I_m^2}{2}} \\ &=\frac{I_m}{\sqrt{2}} \tag{ac.i.2} \end{align} $$

类似地可以计算出

$$ u=U_m\sin(\omega t) \tag{ac.u.1} $$

其中$U_m$为电压的最大值，也称为峰值电压，单位是伏特（Volt）；类似于上面的推导我们可以得出其有效值为:

$$ U_{\mathrm{eff}}=\frac{U_m}{\sqrt{2}} \tag{ac.u.2} $$

相位和初相位：

$$ i=I_m\sin(\omega t+\psi) $$

在这种情况下$i_0=I_m\sin\psi$，$\psi$称为初相位，单位是弧度（radian）；而$\omega t+\psi$称为相位，单位也是弧度。

正弦量的表示，根据欧拉公式：

$$ e^{j\theta}=\cos\theta+j\sin\theta $$

可以将一个特定的正弦量表示为一个复数$A$：

$$ \begin{align} A&=a+jb \ &=rcos\psi+jrsin\psi =r(\cos\psi+j\sin\psi) \ &=r\cdot e^{j\psi} \end{align} $$

或者简写为：

$$ A=r\phase{\psi} $$

其中$r$称为幅值，$\psi$称为相位，$A$称为复数。

由于$\omega$已知在同一个电路中通常是相同的，我们只需要考虑初相位的差异，就可以通过复数表示正弦量，称为相量。

$$ \begin{gather} \dot U = U(\cos\psi + j\sin\psi) = Ue^{j\psi} = U\phase{\psi} \tag{ac.u.3} \\ \dot I = I(\cos\psi + j\sin\psi) = Ie^{j\psi} = I\phase{\psi} \tag{ac.i.3} \end{gather} $$

注意这些标识，我们再来整理一下

量	瞬时值	有效值	峰值	相量
电压	$i$	$U$	$U_m$	$\dot U$
电流	$u$	$I$	$I_m$	$\dot I$

这些标志在后面的分析中会经常用到，千万不要搞混了。

电阻和交流电路

$$ \begin{align} i =\frac{u}{R} &= \frac{U_m}{R}\sin(\omega t) = \sqrt{2}I\sin(\omega t) \tag{ac.r.1} \\ u=Ri &= RI_m\sin(\omega t) \notag \&= \sqrt{2}RI\sin(\omega t)\tag{ac.r.2} \&= \sqrt{2}\red{U}\sin(\omega t)\notag \\ \end{align} $$

由此可见：

1. 频率不变；
2. 大小关系为$U=RI$；
3. 相位关系为$\psi_u=\psi_i$，即相位差$\varphi=\psi_u-\psi_i=0$。
4. 相量关系$\dot U = U\phase{\psi_u} = RI\phase{\psi_i} = R\dot I$
5. 功率关系：

$$ \begin{align} \text{瞬时功率} p &= ui \\ &= \sqrt{2}Isin(\omega t) \cdot \sqrt{2}Usin(\omega t) \\ &= U_mI_m\sin^2(\omega t) \\ &= \frac{U_mI_m}{2}(1-\cos(2\omega t)) \geq 0 \\ \text{平均功率} P&=\frac{1}{T}\int_0^T p\mathrm{d}t \\ &=\frac{U_mI_m}{2}\left(\frac{1}{T}\int_0^T \mathrm{d}t-\frac{1}{T}\int_0^T \cos(2\omega t)\mathrm{d}t\right) \\ &= \frac{U_mI_m}{2}\left(1-\frac{1}{T}\int_0^T \cos(2\omega t)\mathrm{d}t\right) \\ &= \frac{U_mI_m}{2} \\ &= UI = RI^2 = \frac{U^2}{R} \\ \end{align} $$

电感和交流电路

电感的电压电流关系为$u=L\frac{\mathrm{d}i}{\mathrm{d}t}$。代入$(ac.i.1)$，得到：

$$ \begin{align} i&=I_m\sin(\omega t)=\sqrt{2}I\sin(\omega t) \tag{ac.l.1} \\ u&=L\frac{\mathrm{d}i}{\mathrm{d}t} \\ &= \omega LI_m\cos(\omega t) \\ &= \sqrt{2}\omega LI\cos(\omega t) \\ &= \sqrt{2}\omega LI\sin(\omega t+\frac{\pi}{2}) \tag{ac.l.2} \\ &= \sqrt{2}\red{U}\sin(\omega t+\frac{\pi}{2}) \\ \end{align} $$

由此可见：

1. 频率不变；
2. 有效值的关系：$U=I\omega L$或者$I=\frac{U}{\omega L}$；
3. 电压超前电流$\frac{\pi}{2}$，即$\psi_u=\psi_i+\frac{\pi}{2}$，即相位差$\varphi=\psi_u-\psi_i=\frac{\pi}{2}$。

感抗：$X_L=\omega L = 2\pi fL$

则有$U = X_LI$；

注意，感抗只是电压和电流的幅值或者有效值之比，不是瞬时值之比，即$\frac{u}{i}\neq X_L$，事实上电压和电流成导数关系，即$u=X_L\frac{\mathrm{d}i}{\mathrm{d}t} = XI_m\sin(\omega t+\frac{\pi}{2})$。

那么，对于相量，$\dot U = Ue^{j \frac{\pi}{2}}$，$\dot I = Ie^{j 0}$：

$$ \begin{align} \frac{\dot U}{\dot I} &= \frac{Ue^{j \cdot \frac{\pi}{2}}}{Ie^{j \cdot 0}} \\ &= \frac{U}{I}e^{j\cdot \frac{\pi}{2}} \\ &= jX_L \\ \dot U &= j\dot I X_L \\ &= j\dot I \omega L \\ \end{align} $$

功率的计算：

$$ \begin{align} \text{瞬时功率} p &= ui \\ &= \sqrt{2}I\sin(\omega t) \cdot \sqrt{2}U\sin(\omega t+\frac{\pi}{2}) \\ &=2UI\sin(\omega t)\cos(\omega t) \\ &= UI\sin(2\omega t) \\ \text{平均功率} P&=\frac{1}{T}\int_0^T p\mathrm{d}t \\ &=\frac{UI}{2}\left(\frac{1}{T}\int_0^T \sin(2\omega t)\mathrm{d}t\right) \\ &= 0 \\ \end{align} $$

由于电感不消耗能量，所以平均功率为0，只有电源和电感元件之间的能量转化，我们将这种能量转化的规模用无功功率（瞬时功率的幅值）来表示，即：

$$ Q=UI = \frac{U^2}{X_L} = X_LI^2 $$

单位为伏特安培乘以秒，即瓦特秒（Watt second），也称为乏（Var）。

电容和交流电路

电容的电压电流关系为$i=C\frac{\mathrm{d}u}{\mathrm{d}t}$。代入$(ac.u.1)$，得到：

$$ \begin{align} u&=U_m\sin(\omega t)=\sqrt{2}U\sin(\omega t) \tag{ac.c.1} \\ i&=C\frac{\mathrm{d}u}{\mathrm{d}t} \\ &= \omega CU_m\cos(\omega t) \\ &= \sqrt{2}\omega CU\cos(\omega t) \\ &= \sqrt{2}\omega CU\sin(\omega t+\frac{\pi}{2}) \tag{ac.c.2} \\ &= \sqrt{2}\red{I}\sin(\omega t+\frac{\pi}{2}) \\ \end{align} $$

由此可见：

1. 频率不变；
2. 有效值的关系：$I=\omega CU$或者$U=\frac{I}{\omega C}$；
3. 电流超前电压$\frac{\pi}{2}$，即$\psi_i=\psi_u+\frac{\pi}{2}$，即相位差$\varphi=\psi_u-\psi_i=-\frac{\pi}{2}$。

容抗：$X_C=\frac{1}{\omega C} = \frac{1}{2\pi fC}$

则有$U = \frac{I}{X_C}$；

注意，容抗只是电压和电流的幅值或者有效值之比，不是瞬时值之比，即$\frac{u}{i}\neq X_C$，事实上电流和电压成导数关系，即$i=X_C\frac{\mathrm{d}u}{\mathrm{d}t} = XI_m\sin(\omega t+\frac{\pi}{2})$。

那么，对于相量，$\dot U = Ue^{j \frac{\pi}{2}}$，$\dot I = Ie^{j 0}$：

$$ \begin{align} \frac{\dot U}{\dot I} &= \frac{Ue^{j \cdot \frac{\pi}{2}}}{Ie^{j \cdot 0}} \\ &= \frac{U}{I}e^{j\cdot \frac{\pi}{2}} \\ &= -jX_C \\ \dot U &= -j\dot I X_C \\ &= -j \frac{\dot I}{\omega C} \\ &= \frac{\dot I}{j\omega C} \end{align} $$

功率的计算：

$$ \begin{align} \text{瞬时功率} p &= ui \\ &= \sqrt{2}I\sin(\omega t+\frac{\pi}{2}) \cdot \sqrt{2}U\sin(\omega t) \\ &=2UI\sin(\omega t+\frac{\pi}{2})\cos(\omega t) \\ &= -UI\sin(2\omega t) \\ \text{平均功率} P&=\frac{1}{T}\int_0^T p\mathrm{d}t \\ &=\frac{UI}{2}\left(\frac{1}{T}\int_0^T -\sin(2\omega t)\mathrm{d}t\right) \\ &= 0 \\ \text{无功功率} Q&=-UI = -\frac{U^2}{X_C} = -X_CI^2 \end{align} $$

上述三种元器件的串联

分压关系和阻抗三角形、电压三角形

假设一个电路有一个电阻$R$，一个电感$L$，一个电容$C$，并联在一起，电压为$u$，电流为$i$，则有：

$$ \begin{align} u&=Ri+L\frac{\mathrm{d}i}{\mathrm{d}t}+\frac{1}{C}\int i\mathrm{d}t \\ \dot U &= R\dot I + j\omega L\dot I + \frac{\dot I}{j\omega C} \\ &= \dot I\left[R+j\left(X_L-X_C\right)\right] \\ \end{align} $$

将式子里面的$R+j\left(X_L-X_C\right)$记为$Z$，则有：

$$ \begin{align} Z &= R+j\left(X_L-X_C\right) \\ &= \sqrt{R^2+\left(X_L-X_C\right)^2}e^{j\cdot\arctan\frac{X_L-X_C}{R}} \\ &= \red{|Z|}e^{j\red\varphi} \\ \end{align} $$

其中$|Z|$称为阻抗模，$\frac{U}{I} = \sqrt{R^2+\left(X_L-X_C\right)^2} = |Z|$，单位为欧姆（Ohm）；$\varphi$称为阻抗的幅角，$\varphi = \arctan\frac{X_L-X_C}{R}$，单位为弧度，即电流和电压的相位差。

可以将阻抗的复数形式理解为，实部为“阻”，虚部为“抗”，即阻抗的实部为电阻，虚部为电抗，电抗有两种，一种是感抗，一种是容抗；既表示了大小关系$|Z|$，也表示了相位关系$\varphi$。

功率的计算与功率三角形

$$ \begin{align} \text{对于} \\ i&=I_m\sin(\omega t) \\ u&=U_m\sin(\omega t+\varphi) \\ \text{瞬时功率} p &= ui \\ &= U_mI_m\sin(\omega t+\varphi)\sin(\omega t) \\ &= UI\cos(\varphi) - UI \cos(2\omega t+\varphi) \\ \text{平均功率} P&=\frac{1}{T}\int_0^T p\mathrm{d}t \\ &= \frac{1}{T} \int_0^T \left[UI\cos(\varphi) - UI \cos(2\omega t+\varphi)\right] \mathrm{d}t \\ &= \frac{1}{T} \left[UI\cos(\varphi)\int_0^T \mathrm{d}t - UI \int_0^T \cos(2\omega t+\varphi)\mathrm{d}t\right] \\ &= \frac{1}{T} \left[UI\cos(\varphi)T-0\right] \\ &= UI\cos\varphi \\ \text{无功功率} Q&=U_LI-U_CI = X_LI^2-X_CI^2 = |Z|I^2\sin\varphi = UI\sin\varphi \end{align} $$

可见，功率不仅与电源（发电机）的端电压和输出电流的有效值的乘积有关，还与负载的参数有关（因为负载会影响到$\varphi$），我们称$\cos(\varphi)$为功率因数 。

定义视在功率： $S=UI=|Z|I^2$

如果用直角三角形描述这个功率的关系，可以得到：

阻抗的串并联

串联

$$ Z = \sum Z_k = \sum R_k + j \sum X_k =|Z|e^{j\varphi} = |Z|\phase{\varphi} $$

并联

$$ \frac{1}{Z} = \sum \frac{1}{Z_k} $$

三相交流电

三相电压频率相同、相位差为 $\frac{2\pi}{3}$ 的三个正弦电压称为三相电压，三相电压的有效值相等，称为对称三相电压。

三相电路的连接方式分为：

1. 星形连接（Y形连接）
2. 三角形连接

相电压与线电压

发电机通常使用星形连接，即将三个末端连在一起，这个点称为中性点，中性点引出的导线称为中性线（或者零线），从始端引出的三根导线称为相线或者端线（俗称火线），中性线与任意一个相线的电压称为相电压，相电压的有效值一般记作$U_P$；任意两端间的电压称为线电压，线电压的有效值为$U_L$。

用相量表示相电压和线电压：

$$ \begin{align} \dot U_{12} = \dot U_1 - \dot U_2 \\ \dot U_{23} = \dot U_2 - \dot U_3 \\ \dot U_{31} = \dot U_3 - \dot U_1 \\ \end{align} $$

容易求出，相电压的矢量差为线电压，线电压超前于相电压 $\frac{\pi}{6}$，并且有效值的大小关系为：

$$ \begin{align} U_P = \frac{U_L}{\sqrt{3}} \\ U_L = \sqrt{3}U_P \end{align} $$

在中国大陆地区，三相电压的有效值为 $220V$，线电压的有效值为 $380V \approx \sqrt{3} \times 220$。

负载星形连结

在三相四线制中，很显然相电流和线电流是相同的。

设电源的相电压分别为$\dot U_1 = U_1 \phase 0^\circ$，$\dot U_2 = U_2 \phase{-120^\circ}$，$\dot U_3 = U_3 \phase{120^\circ}$，负载的阻抗分别为$\dot Z_1 = Z_1 \phase{\varphi_1}$，$\dot Z_2 = Z_2 \phase{\varphi_2}$，$\dot Z_3 = Z_3 \phase{\varphi_3}$，则三个相电流的相量为：

$$ \begin{align} \dot I_1 &= \frac{\dot U_1}{\dot Z_1} = \frac{U_1}{|Z_1|} \phase{-\varphi_1} \\ \dot I_2 &= \frac{\dot U_2}{\dot Z_2} = \frac{U_2}{|Z_2|} \phase{-120^\circ-\varphi_2} \\ \dot I_3 &= \frac{\dot U_3}{\dot Z_3} = \frac{U_3}{|Z_3|} \phase{120^\circ-\varphi_3} \\ \text{其中} \\ \varphi_1 &= \arctan \frac{X_1}{R_1} \\ \varphi_2 &= \arctan \frac{X_2}{R_2} \\ \varphi_3 &= \arctan \frac{X_3}{R_3} \\ \end{align} $$

中性线的电流$\dot I_N = \dot I_1 + \dot I_2 + \dot I_3$。

当负载均衡时，即$Z_1 = Z_2 = Z_3$，则$\varphi_1 = \varphi_2 = \varphi_3$，此时中性线的电流为零。

这个时候中性线就可以被拆除，这样就可以节省一根导线，这种连接方式称为三相三线制。这种情况一般见于对称的三相负载，比如三相电机。

对于负载不均衡的情况，使用相量分别计算即可。

当出现负载短路时，考虑到短路处的电流过大导致熔断，此时这个支路其实断开而其他支路不受影响；对于中性线断开的情况（或者说三相三线制），未短路的两个支路相当于串联接在了线电压上。

负载三角形连结

三角形连结是指将三个负载分别连接在三相电源的三个相线上。

各相负载的电流有效值为：

$$ \begin{align} I_{12} &= \frac{U_{12}}{|Z_{12}|} \\ I_{23} &= \frac{U_{23}}{|Z_{23}|} \\ I_{31} &= \frac{U_{31}}{|Z_{31}|} \\ \end{align} $$

相位差：

$$ \begin{align} \varphi_{12} &= \frac{X_{12}}{R_{12}} \\ \varphi_{23} &= \frac{X_{23}}{R_{23}} \\ \varphi_{31} &= \frac{X_{31}}{R_{31}} \\ \end{align} $$

负载的线电流根据基尔霍夫定律，有：

$$ \begin{align} \dot I_1 &= \dot I_{12} - \dot I_{31} \\ \dot I_2 &= \dot I_{23} - \dot I_{12} \\ \dot I_3 &= \dot I_{31} - \dot I_{23} \\ \end{align} $$

当负载均衡时，即$Z_{12} = Z_{23} = Z_{31}$，则$\varphi_{12} = \varphi_{23} = \varphi_{31}$，此时：

$$I_{12} = I_{23} = I_{31} = I_P = \frac{U_P}{|Z|}$$

$$\varphi_{12} = \varphi_{23} = \varphi_{31} = \varphi = \arctan\frac{X}{R}$$

此时，线电流和相电流的关系为：

• 线电流相位比相电流滞后 $\frac{\pi}{6}$
• 大小关系：$I_L = \sqrt{3}I_P$

功率

总功率是三个相功率之和，当负载均衡时，三个相功率相等：

$$ P = 3 P_P = 3 U_P I_P \cos \varphi \tag{ac.3.P.1} $$

• 负载星形连结时

$$ U_L = \sqrt{3} U_P \qquad I_L = \sqrt{3} I_P $$

• 负载三角形连结时

$$ U_L = U_P \qquad I_L = \sqrt{3} I_P $$

代入 $(ac.3.P.1)$ 式，得到：

$$ P = \sqrt{3} U_L I_L \cos \varphi \tag{ac.3.P.2} $$

同理，视在功率和无功功率也可以得到类似的关系：

$$ \begin{align} S &= \sqrt{3} U_L I_L \\ Q &= \sqrt{3} U_L I_L \sin \varphi \end{align} $$

交流电的小结

• 相电压（$U_P$）的有效值相等，称为对称三相电压
• 三相电路的连接方式分为星形连接（Y形连接）和三角形连接
• Y连接时三相电压的相量差为线电压（$U_L$），线电压超前于相电压 $\frac{\pi}{6}$，并且有效值的大小关系为：$U_P = \frac{U_L}{\sqrt{3}}$；相电流和线电流相等
• 负载Y形连接，就是三相四线制；负载均衡时，三相电路的中性线电流为零，此时可以拆除中性线，这种连接方式称为三相三线制
• 负载三角形连接，三相电路的线电流和相电流的关系为：$I_L = \sqrt{3} I_P$，线电流相位比相电流滞后 $\frac{\pi}{6}$

磁路

基本物理量

• 磁感应强度：$B$，单位：$T$（特斯拉）
• 磁通量：$\Phi=BS$，单位：$Wb$（韦伯）
• 磁场强度：$H=\frac{B}{\mu}$，单位：$A/m$（安培/米）
• 磁导率：$\mu=\frac{B}{H}$，单位：$H/m$（亨利/米）
• 真空磁导率：$\mu_0=4\pi \times 10^{-7} H/m$； 相对磁导率：$\mu_r=\frac{\mu}{\mu_0}=\frac{B}{B_0}$

安培环路定理

$$ \oint \vec H \cdot \mathrm d \vec l = \sum \vec H \cdot \mathrm d \vec l = NI $$

即，磁场强度沿闭合回路的线积分等于回路上的电流的代数和。

磁饱和与磁滞性

磁饱和：当磁场强度增加时，磁感应强度不再增加，称为磁饱和。

磁滞性：磁滞性是指材料中磁感应强度总是滞后于外磁场强度的变化的性质。

根据磁性能，磁性材料分为：

• 软磁材料：磁滞回线较窄，矫顽磁力较小
• 永磁材料：磁滞回线较宽，矫顽磁力较大
• 矩磁材料：磁滞回线近乎矩形，剩磁大，矫顽磁力小，稳定性良好。

电磁关系

主磁通$\Phi$、漏磁通$\Phi_\sigma$与电动势的关系：

$$ \begin{gather} e=-N\frac{\mathrm d \Phi}{\mathrm d t} \tag{ac.4.1} \\ e_\sigma = -N\frac{\mathrm d \Phi}{\mathrm d t} \tag{ac.4.2} \end{gather} $$

根据KVL：

$$ u=Ri-e-e_\sigma \tag{ac.4.3} $$

其中 $R$ 为线圈导线的电阻。

如果忽略电阻和漏磁通，

$$ \begin{align} \dot U&=R\dot I-\dot E-\dot E_\sigma \\ &\approx - \dot E \end{align} $$

功率损耗：

• 铜损：$P_{Cu}=RI^2$

  其中 $R$ 为线圈导线的电阻，$I$ 为线圈电流的有效值。

• 铁损：$P_{Fe}=K_f\Phi^2$

  • 铁损中的磁滞损耗：$\Delta P_h$
  • 铁损中的涡流损耗：$\Delta P_e$

变压器

电压变换关系

$$E_1 = \frac{ {E_1}_m}{\sqrt{2}} = \frac{2\pi f N_1 \Phi_m}{\sqrt{2} } = 4.44 f N_1 \Phi_m$$

同理，$E_2 = 4.44 f N_2 \Phi_m$。

根据KVL：

$$ \begin{align} \dot U_1 &= R_1\dot I_1 -\dot E_{\sigma 1} - \dot E_1 \approx - \dot E_1 \\ U_1 &\approx E_1 = 4.44 f N_1 \Phi_m \\ \dot E_2 &= R_2\dot I_2 -\dot E_{\sigma 2} + \dot U_2 \\ \text {当变压器空载时，} \dot I_2 &= 0 \\ U_{20} = U_2 &= \dot E_2 = 4.44 f N_2 \Phi_m \end{align} $$

匝比（变比）：

$$ \frac{U_1}{U_{20}} \approx \frac{E_1}{E_2} = \frac{N_1}{N_2} = K $$

三相变压器的 $Y$ / $Y_0$ 连接

线电压之比也等于匝比：

$$ \frac{U_{1}}{U_{2}} = \frac{\sqrt{3}{U_P}_1}{\sqrt{3}{U_P}_2} = K $$

三相变压器的 $Y_0$ / $\Delta$ 连接

线电压之比：

$$ \frac{U_{1}}{U_{2}} = \frac{\sqrt{3}U_{P1}}{U_{P2}} = \sqrt{3}K $$

电流变换

结论：变压器的电流变换比等于电压变换比的倒数$\frac{1}{K}$。

阻抗变换

电压为$K$倍，电流为$\frac{1}{K}$倍，阻抗为$K^2$倍。

变压器型号

例子：SJL-1000/10，其中：

• S：三相（D：单相）
• J：油浸自冷式
• L：铝线圈
• 1000：额定容量为$1000kVA$
• 10：高压绕组的额定电压为$10kV$

额定值

• 额定电压${U_1}_N$、${U_2}_N$：

  • 单相：${U_1}_N$，一次侧的电压；${U_2}_N$，二次侧的空载的电压
  • 三相：${U_1}_N$，一次侧的线电压；${U_2}_N$，二次侧的线电压

• 额定电流${I_1}_N$、${I_2}_N$：

  • 单相：${I_1}_N$，一次侧的电流；${I_2}_N$，二次侧的电流
  • 三相：${I_1}_N$，一次侧的线电流；${I_2}_N$，二次侧的线电流

• 额定容量$S_N$：

  • 单相：$S_N = {U_2}_N {I_2}_N \approx {U_1}_N {I_1}_N$
  • 三相：$S_N = \sqrt{3} {U_2}_N {I_2}_N \approx \sqrt{3} {U_1}_N {I_1}_N$

  输出功率$P_2 = U_2 I_2 \cos \varphi_2$，其中$\varphi_2$为二次侧的功率因数。

  一次侧的输入功率$P_1 = P_2 + P_{Fe} + P_{Cu}$，其中$P_{Fe}$为铁损，$P_{Cu}$为铜损。

  $\eta = \frac{P_2}{P_1}$，称为变压器的效率，一般$\eta > 0.95$；负载在额定容量的$50~75%$时，效率最高。

• 额定频率$f_N$：$50Hz$或者$60Hz$

特殊变压器

• 自耦变压器：一次侧和二次侧共用一部分线圈，一般用于降压
• 电流互感器：一般用于测量电流

交流电动机

graph LR
A[电动机] --> B[交流电动机]
B --> E[异步电动机]
B --> F[同步电动机]
E --> G[三相电动机]
E --> H[单相电动机]
A --> C[直流电动机]

Loading

旋转磁场

定子三相绕组通入三相交流电。三相交流电的相位差为 $\frac{2\pi}{3}$，这个相位差导致了连接在三相绕组的三个线圈相位有规律的变化，可以视为是在“旋转”，因此导致了内部转子跟着旋转起来。就是说定子没有转，但是电流在周期性变化，就和“电流不变而定子在转”等效。

如果需要调节电机的旋转方向，就需要对其两根进线进行调换，这样形成的磁场和调换之前的恰好相反，也就使得电机能反转。

旋转磁场的极对数$P$与三相绕组的排列有关。转速与极对数的关系：

$$ n_0=\frac{60f_1}{p} $$

单位：转/分

转差率

电动机转子和磁场旋转方向一致，但是$n < n_0$，这个差值称为转差率，这是因为转子的转动是磁通切割转子的导条，这个前提就是二者不是完全同步的。转差率：

$$ s=\left(\frac{n_0-n}{n_0}\right) \times 100% $$

也可以写作：$n=(1-s)n_0$

异步电机运行中，一般$s=(1\sim 9)%$。

含三相异步电机的电路分析

三相异步电机的电磁关系和变压器类似。

旋转磁场的磁通$\Phi$：

$$ \begin{gather} U_1 \approx E_1 = 4.44 f_1 N_1 \Phi \notag\\ \Phi \approx \frac{U_1}{4.44 f_1 N_1} \notag \end{gather} $$

定子感应电动势的频率（等于电源的频率）：

$$f_1=\frac{pn_0}{60}$$

转子的感应电动势频率：

$$f_2 = \frac{n_0-n}{60} p =sf_1 \neq f_1$$

转子感应电动势：

$$E_2 = 4.44 f_2 N_2 \Phi = 4.44 sf_1 N_2 \Phi$$

当转速$n=0$ 时，$f_2$最大，此时$E_2$最大，记为$E_{20}$，即：

$$ \begin{gather} E_{20} = 4.44 f_1 N_2 \Phi \notag\\ E_2 = sE_{20} \notag \end{gather} $$

转子的感抗$X_2$：

$$ X_2 = 2\pi f_2 L_{\sigma 2} = 2 \pi sf_1 L_{\sigma 2} $$

类似的，$n=0$ 时，$X_2$最大，记为$X_{20}$，即：

$$ \begin{gather} X_{20} = 2 \pi f_1 L_{\sigma 2} \notag\\ X_2 = sX_{20} \notag \end{gather} $$

转子电流：

$$ \begin{align*} I_2 = \frac {E_2}{\sqrt{R_2^2 + X_2^2}} = \frac{sE_{20}}{\sqrt{R_2^2 + s^2X_{20}^2}} \\ \left \lbrace \begin{aligned} s&=0 \rightarrow I_2 = 0 (n=n_0) \ s&=1 \rightarrow I_2 = \frac{E_{20}}{\sqrt{R_2^2 + X_{20}^2}} (n=0) \end{aligned} \right. \end{align*} $$

功率因素：

$$ \cos \psi_2 = \frac{R_2}{\sqrt{R_2^2 + X_2^2}} = \frac{sX_{20}}{\sqrt{R_2^2 + s^2X_{20}^2}} $$

• 当$s$很小时，$\cos \varphi_2 \approx 1$，功率因数接近于1，电机效率高；
• 当$s$很大时，$\cos \varphi_2 \propto \frac{1}{s}$，电机效率低。

我们分析可知，这上面的所有物理量都与转差率，或者说与转速有关

转矩

转矩公式

$$ T=K_T I_2 \Phi \cos(\psi_2) = K \frac{sR_2}{R_2^2 + s^2X_{20}^2} U_1 ^2 \tag{ac.5.1} $$

• 额定转矩$T_N$： $$T = \frac{P}{\frac{2\pi n}{60}} = 9550 \frac{P}{n}$$ 那么额定转矩$T_N = 9550 \frac {P_N}{n_N}$ 单位：$N \cdot m$
• 最大转矩$T_{max}$： 令$\frac{\mathrm d T}{\mathrm d s} = 0$，得到$S=S_m = \frac{R_2}{X_20}$，代入转矩公式 $$ T_{max} = K \frac{U_1^2}{2X_{20} } $$ 负载转矩不得大于最大转矩，否则堵转。
• 过载系数 $$ \lambda = \frac{T_{max} }{T_N} $$ 一般$\lambda$在1.8~2.2
• 起动转矩$T_{st}$ 起动时$n=0$，$s=1$，代入转矩公式， $$ T_{st} = K \frac{R_2 U_1^2}{R_2^2 + X_{20}^2} $$ 若$T_{st} > T_2$则电动机可以起动，否则不能。
• 起动能力 $$ K_{st} = \frac{T_{st} }{T_N} $$

转矩平衡条件：

• 转子轴上的转矩$T_2 = T - T_0$，其中$T_0$为转子的机械转矩
• 空载转矩：$T_0$
• 输出转矩：$T_2 = T - T_0 \approx T$
• 负载转矩：$T_Z$
  • 当$T_Z = T_2$时，电动机处于稳定转速
  • 当$T_Z > T_2$时，电动机加速
  • 当$T_Z < T_2$时，电动机减速

负载对电动机运行的影响：电动机的电磁转矩随负载变化自动调整，称为自适应负载能力。

$U_1$对机械特性的影响：随着$U_1$减小，$T_{max}$减小，$T_{st}$减小。

起动

• 直接起动： 电动机的起动电流很大，会导致电网电压下降，影响其他设备的正常运行，因此不常用。
• 降压启动： 通过星形-三角形换接，或者自耦降压
• 转子串电阻起动： 绕线式电机

降压启动

星形-三角形换接

三角形连结时，$I_{l\Delta } = \sqrt{3}\frac{U_l}{Z}$

星形连结时，$I_{lY} = \frac{U_l}{\sqrt{3}Z}$

因此，降压起动，电流为三分之一

类似地，$T_{stY} = \frac{1}{3}T_{st\Delta}$

• 仅适用于正常运行为三角形连结的电动机
• 换接适用于轻载或者空载

自耦降压起动

• 适用于容量大、或者正常运行时为Y连结而不能使用$Y-\Delta$起动的鼠笼式异步电动机

电机调速

• 无极调速：改变电源频率
• 变极调速：改变极对数$P$，改变电机的转速

制动

• 能耗制动：断开交流电流，通入直流电流
• 反接制动：将电动机的两根进线交换，使得电动机反转，此时电动机的转矩方向与负载转矩方向相反，从而实现制动
• 发电反馈制动：电动机转子速度大于旋转磁场速度，驱动转矩变为制动转矩

铭牌数据

例子：Y132M-4，其中：

• Y：三相异步电动机
• 132：基座中心高，单位：$mm$
• M：基座长度代号，单位：$mm$
• 4：磁极数（极对数的两倍）

其他内容参考课本，这里不再赘述。

模拟电路

半导体器件

本证半导体、杂质半导体和PN结

本征半导体：在半导体中，每个原子都有四个价电子，当半导体中的原子数目足够多时，每个原子都可以与四个相邻原子共享一个价电子，形成共价键，这样的半导体称为本征半导体。

杂质半导体：在半导体中，掺入少量杂质，使得半导体中的原子数目不足以与相邻原子共享四个价电子，这样的半导体称为杂质半导体。分为N型半导体和P型半导体。

N型半导体：掺入的杂质原子有五个价电子（如磷、砷、锑），其中四个价电子与相邻原子共享，而剩下的一个价电子处于自由状态，这样的半导体称为N型半导体。

P型半导体：掺入的杂质原子有三个价电子（如硼、镓、铟），其中三个价电子与相邻原子共享，而剩下的一个价电子处于缺电子状态，这样的半导体称为P型半导体。

PN结：将N型半导体和P型半导体的晶体片背靠背地粘合在一起，使得P型半导体中的自由电子与N型半导体中的空穴结合，形成一个电子云，这样的结构称为PN结。

PN结具有单向导电性，当 P 接入正电压，N 接入负电压时，正向电流较大、电阻较小，为导通状态（正向偏置）；当 P 接入负电压，N 接入正电压时，正向电流较小、电阻较大，为截止状态（反向偏置）。

温度越高，反向电流越大。

二极管分为：点接触型、面接触型、平面型。

二极管的伏安特性

主要参数：

• 最大整流电流$I_{OM}$：允许流过二极管的最大正向电流。
• 反向工作峰值电压$U_{RWM}$：保证二极管在反向工作时不会击穿的最大反向电压。
• 最大反向电流$I_{RM}$：二极管加最高反向电压时的反向电流。

二极管小结

• 正向偏置：正向导通，正向的电阻较小，正向的电流较大
• 反向偏置：反向截止，反向的电阻较大，反向的电流较小
• 反向击穿：反向电压超过反向工作峰值电压时，二极管会击穿，反向电流急剧增大，二极管会被烧毁

二极管的反向电流受温度影响较大，温度越高反向电流越大。

对于理想二极管，正向导通的时候压降为0，反向截止的时候二极管相当于断开。

二极管的分析方法：将其视为断路，比较两侧的电势。

稳压二极管

文雅二极管在工作时加反向电压。工作状态为反向击穿，此时电压变化很小但是电流变化较大，使用时应加限流电阻。

主要参数：

• 稳定电压$U_Z$：稳压二极管在工作时（反向击穿）的电压。
• 电压温度系数$\alpha_U$：环境温度每变化 1 开尔文，稳压二极管的稳定电压变化的百分比。
• 动态电阻$r_z = \frac{\Delta U_Z}{\Delta I_Z}$：稳压二极管在工作时的动态电阻，$r_Z$ 越小，稳压性能越好。
• 最大稳定电流$I_{ZM}$、稳定电流$I_Z$
• 最大允许耗散功率$P_{ZM} = U_Z I_{ZM}$

三极管

三极管的结构

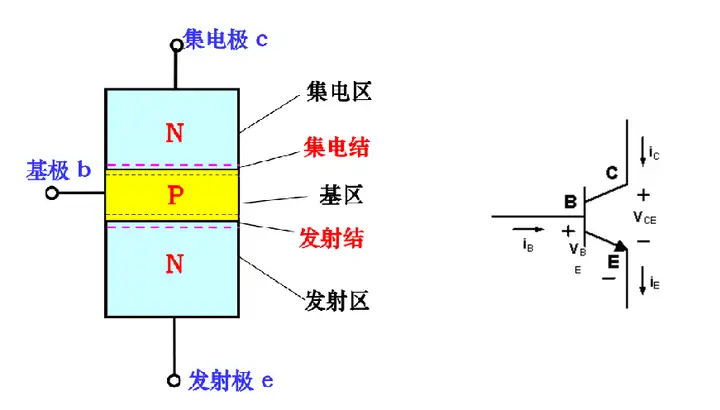
• NPN 三极管：P 型半导体夹在两个 N 型半导体之间
• PNP 三极管：N 型半导体夹在两个 P 型半导体之间

三极管电流分配和放大原理

三极管的电流关系：

$$ I_E = I_B + I_C $$

因为$I_B $远小于$ I_C$，所以可以近似认为$I_E \approx I_C$。定义静态电流放大系数：

$$\bar \beta = \frac{I_C}{I_B} $$

动态电流放大率，基极电流的较小的变化放大为集电极电流较大的变化：

$$ \beta = \frac{\Delta I_C}{\Delta I_B} $$

三极管内部载流子的运动规律

以 NPN 型三极管为例，发射结正向偏置，集电结反向偏置。

1. 发射结正向偏置，发射区的电子扩散进入基区，并不断从电源获取新的电子，形成发射极电流$I_E$；由于基区的空穴浓度比发射区的自由电子浓度小得多，空穴向发射极的扩散忽略不计；
2. 发射区扩散到基区的电子主要聚集在发射结，而靠近集电结的电子密度较低，因而自由电子会继续向集电结扩散，过程中不断与基区的空穴结合；由于基区接电源的正极，基区中的电子不断被拉走，使得基区的空穴不断得到补充，形成了电流$I_{BE}$——基本上等于基极电流$I_B$；由于基区很薄而且掺杂度不高，绝大部分的电子都最终到了集电结的边缘；
3. 由于集电结的反偏，阻挡了集电区的自由电子往基区扩散，但是能反过来把发射区扩散上来的自由电子拉到几点去，形成了集电极电流$I_{CE}$——基本上等于集电极电流$I_C$；除此以外，集电区的少数载流子（空穴）和基区的少数载流子（自由电子）相向运动，形成了少量的集电极电流$I_{CBO}$——数值很小因为都是少数载流子，但是受温度影响很大而且与外界电压关系不大。

严格意义上，三极管的电流关系为：

$$ \bar \beta = \frac{I_{CE}}{I_{CB}} = \frac{I_{C} - I_{CBO}}{I_{CBO} + I_{B}} \approx \frac{I_{C}}{I_{B}} $$

根据已知，$I_C$远大于$I_B$，而且对于一个很小的$\Delta I_B$，会引起一个很大的$\Delta I_C$。

小结

外部条件：发射结正向偏置，集电结反向偏置。

NPN 型三极管，集电极电位最高，发射极电位最低；PNP 型三极管，集电极电位最低，发射极电位最高——而且都是负值，因为电流从发射极流入，方向和 NPN 是反的。

三极管的伏安特性曲线

探究共发射极接法的特性曲线。

对于上述电路图，输入特性曲线（非线性）：

对于$U_{CE}$为常数时，基极电流$I_B$随$U_{BE}$的变化关系

当发射结电压大于死区电压时才会出现$I_B$

输出特性

1. 放大区
   在放大区，$I_C = \beta I_B$，为线性区，具有恒流源特性。放大区，发射结正偏，集电结反偏。
2. 截止区
   $I_B &lt; 0$，有$I_C = 0$，为截止区，具有开路特性。截止区，发射结反偏，集电结反偏。
3. 饱和区
   $U_{CE} \leq U_{BE}$，有$\beta I_B \geq I_C$，为饱和区，发射结正偏，集电结正偏。

基本放大电路

实质是将小能量的信号通过三极管的控制作用，将放大电路直流电源的能量转化为交流输出。

对放大电路的要求：

• 要有合理的放大倍数
• 尽可能小的波形失真

放大电路的静态分析

放大电路无信号输入时的电路状态。

$$ U_{CC} = U_{CE} + I_CR_C $$

$$ I_B = \frac {U_{CC} - U_{BE}}{R_B} \approx \frac {U_{CC}}{R_B} $$

$$ I_C = \beta I_B $$

放大电路的动态分析

放大电路有（交流）信号输入时的电路状态。此时电容视为短路，并简化电路图为：

输入回路，对于一个极小的$\Delta U{BE}$，近似认为晶体管电流的变化量与其线性相关，即：

$$ r_{BE} = \frac{\Delta U_{BE}}{\Delta I_B} \Big |{U{CE} } = \frac {u_{be}}{i_b} \Big |{U{CE} } $$

对于小功率二极管，$r_{BE} \approx 200 \Omega + (1+\beta) \frac {26 mV}{I_E}$，其中$\beta$为静态电流放大系数，$I_E$为静态电流。

对于输出回路，晶体管放大系数$\beta$：

$$ \beta = \frac{\Delta I_C}{\Delta I_B} \Big |{U{CE} } = \frac {i_c}{i_b} \Big |{U{CE} } $$

一般情况下，$\beta$在20~200之间。

输出电阻（阻值很高）：

$$ r_{CE} = \frac{\Delta U_{CE}}{\Delta I_C} \Big |{I_B} = \frac {u{ce}}{i_c} \Big |_{I_B} $$

因此，对于微变，将晶体三极管可等效为：

使用相量推导电压放大倍数$A_u$：

$$ \begin{align*} A_u &= \frac{\dot U_{o}}{\dot U_{i}} \\ &= \frac{-\beta \dot I_b r_{ce}}{\dot I_b r_{be}} \\ &= -\beta \frac{r_{ce}}{r_{be}} \end{align*} $$

其中$r_{ce}$为$R_C$与$R_L$并联后的电阻。如果$R_L$未接入（断路），则$A_u = -\beta \frac{R_C}{r_{be}}$。

对于输入电阻，$r_i = \frac {\dot U_i}{\dot I_i}$，希望信号源获得的输入电流足够小，因此输入电阻应较大。

由于$r_i$为$R_B$与$r_{be}$并联后的电阻，当$R_B$很大时，$r_i \approx r_{be}$。

对于输出电阻，$r_o = \frac {\dot U_o}{\dot I_o}$。输出电阻表示了放大电路带负载的能力。一般希望较小的输出电阻。

要求$r_i$，一般先断开负载$R_L$，另输入电压为0，外加电压$\dot U_o$，求$\dot I_o$：

$$ \begin{gather} \dot I_o = \dot I_c + \dot I_{R_C} \\ \dot I_b = 0 \\ \dot I_c = 0 \\ r_o = \frac {\dot U_o}{\dot I_o} = \frac {\dot U_o}{\dot I_{R_C}} = R_C \end{gather} $$