Foundation

Formalizing mathematical logic in Lean 4.

Structure & Summary

Main results of this repository. More detailed explanations are provided in the Book and Doc.

• FirstOrder: First-Order Logic and Arithmetic
  • Completeness Theorem
  • Cut-elimination of first-order sequent calculus (Gentzen's Hauptsatz)
  • Arithmetic
  • Gödel's First and Second Incompleteness Theorems
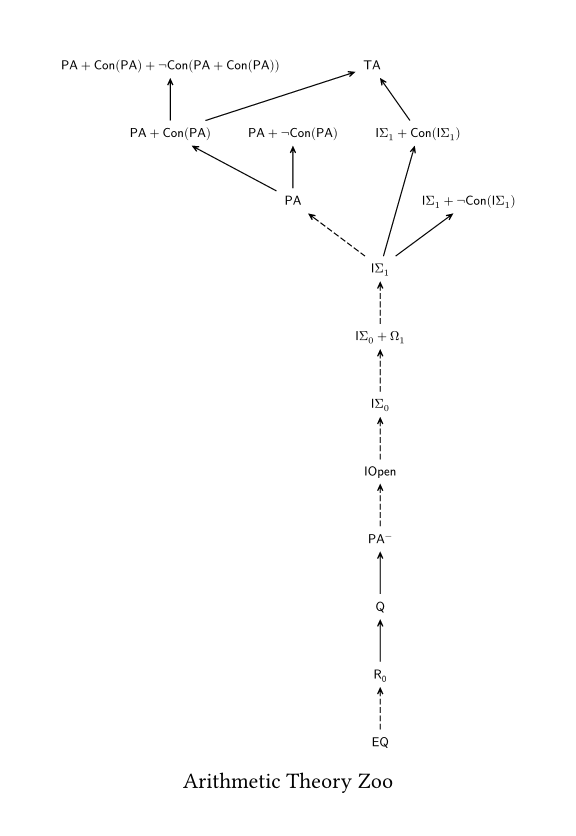
  • Arithmetic Theory Zoo
• IntFO: Intuitionistic First-Order Logic
  • Gödel-Gentzen Translation
• Modal: Basic Modal Logic (with modal operators $\Box, \Diamond$)
  • Kripke completeness for well-known subsystems
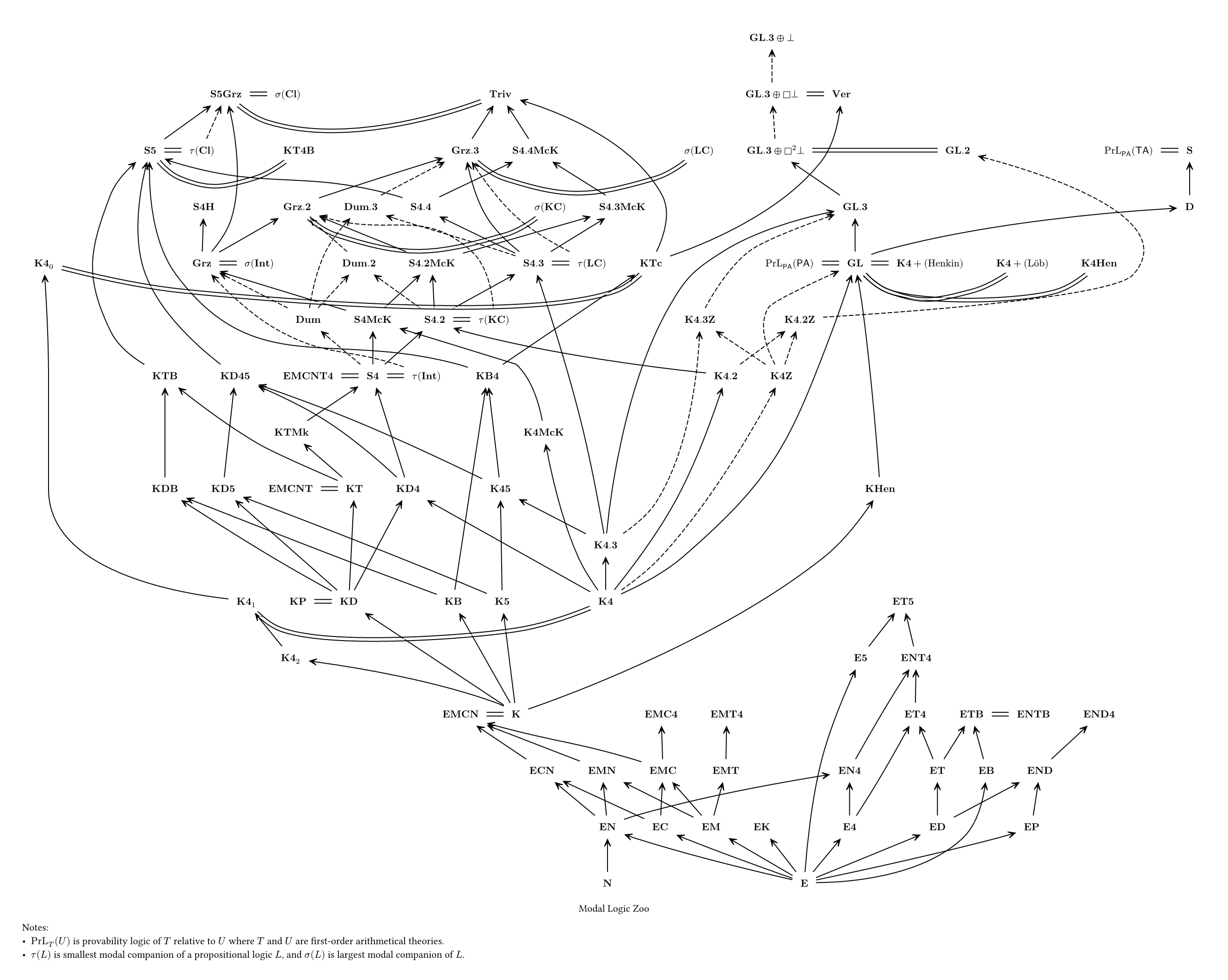
  • Modal Logic Zoo
  • Gödel-McKinsey-Tarski Theorem and Modal Companions
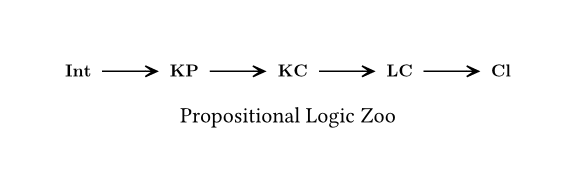
• Propositional: Propositional Logic
  • Tait-style calculus and completeness
  • Completeness for Kripke semantics
  • Disjunctive Property of intuitionistic logic
  • Propositional Logic Zoo
• ProvabilityLogic: Provability Logic
  • Solovay's Arithmetical Completeness Theorem for GL
• Meta: Proof automation.
• Logic: Fundamental tools for various logics.
• Vospiel: Supplemental definitions and theorems for mathlib.

Documents

• Book, summary of results, generated by verso.
• Doc, catelogue of definitions and theorems, generated by doc-gen4.

Zoo

Automatically generated diagrams "Zoo", illustrate the Lean4-verified interrelationships among proof systems.

• A solid arrow $\mathsf{A} \rightarrow \mathsf{B}$ indicates that $\mathsf{B}$ is strictly stronger than $\mathsf{A}$; that is, $\mathsf{B}$ is stronger than $\mathsf{A}$, while $\mathsf{A}$ is not stronger than $\mathsf{B}$, in terms of provability strength.
• A dashed arrow $\mathsf{A} \dashrightarrow \mathsf{B}$ indicates that $\mathsf{B}$ is stronger than $\mathsf{A}$ in terms of provability strength.
• A double line $\mathsf{A} \xlongequal{} \mathsf{B}$ indicates that $\mathsf{A}$ and $\mathsf{B}$ are equivalent in terms of provability strength.

Arithmetic Theory Zoo

Modal Logic Zoo

Propositional Logic Zoo

Build

Book

Book is automatically generated by verso.

Follow the instruction in Book/README.md and build. Some tools e.g. miniserve or python3 -m http.server are useful for check locally.

lake exe book

miniserve _out/html-multi --index index.html

Developers

List of contact information and areas of expertise of the current main developers. If you have any interest or questions, create a new issue or contact us directly.

• Palalansoukî (Shogo Saito, @iehality, ✉️:[email protected])
  • Overall design and maintenance.
  • First-order logic.
  • Intuitionistic first-order logic.
  • Proof automation.
  • Provability logic.
• SnO2WMaN (Mashu Noguchi, @SnO2WMaN, ✉️:[email protected])
  • Modal logic.
  • Propositional logic (including intermediate logic).
  • Provability logic.
  • Miscellaneous repository maintenance (e.g. GitHub Actions)

If you with to cite this repository in academic papers, refer to CITATION.cff.

Financial Supports

Any financial supports would be grateful. If you considered, please contact us.

Previous Sponsors

Companies and organizations that have supported us in the past.

• Proxima Technology (2024-2025)